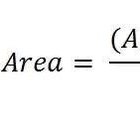Cómo calcular el coeficiente de Poisson
Escrito por Skip Shelton ; última actualización: February 01, 2018
La expresión matemática de la taza de Poisson es utilizada para comprender el efecto de adelgazamiento de un objeto a medida que es estirado. La pregunta fue hecha por el matemático francés Simeon Poisson, y la ecuación recibió el nombre como reconocimiento por su trabajo. La ecuación matemática mide cómo se comprime el material transversalmente mientras es sometido a fuerzas longitudinales. La proporción se expresa como ""υ = - εt / εl", donde "u" es el coeficiente de Poisson, "εt" es la fuerza transversal y " εl" es la fuerza longitudinal.
Mide la longitud y el ancho del objeto original.
Estira el objeto. Mide la longitud y el ancho del objeto estirado.
Calcula la fuerza en las dimensiones físicas del objeto al utilizar la fórmula "ε = dl / L". La fuerza o esfuerzo "ε" es equivalente al cambio en la longitud o "dl", dividido por la longitud inicial o "L". En el coeficiente de Poisson, el área comprimida del objeto es conocida como el esfuerzo transversal y es un número negativo. El área que se estira es conocida como el esfuerzo longitudinal y es un número positivo.
Divide el esfuerzo transversal o negativo por el esfuerzo axial o positivo para generar el coeficiente. Este valor es el coeficiente de Poisson. La expresión original "υ = - εt / εl" puede leerse como: "El coeficiente de Poisson es equivalente al esfuerzo transversal negativo sobre el esfuerzo longitudinal positivo".