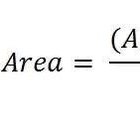Cómo calcular el módulo de rigidez
Escrito por Brad Painting ; última actualización: February 01, 2018
El módulo de rigidez o módulo de cizalladura es un número obtenido experimentalmente que representa el grado de elasticidad que un material muestra bajo una tensión de cizallamiento. El módulo de cizallamiento es importante para varios problemas de ingeniería, tales como la pregunta acerca de cuánto producirá un conjunto de conexiones en un vehículo cuando está cargado. La fórmula para el módulo de rigidez es la tensión de cizallamiento de un material dividido por la deformación del esfuerzo cortante. El proceso varía un poco, dependiendo de si la tensión de cizallamiento es debida a una fuerza lineal o al torque.
Instrucciones para la fuerza lineal
Dibuja un diagrama de cuerpo libre. Un diagrama de cuerpo libre es un dibujo esquemático que muestra el objeto de interés aislado de las piezas circundantes. En lugar de dibujar las partes externas u objetos, reemplázalas con las representaciones de las fuerzas vectoriales que crean.
Calcula la cantidad de fuerza de cizallamiento que actúa sobre cualquier sección transversal del objeto. Ésto es simplemente una cuestión de buscar en tu diagrama de cuerpo libre y sumar o restar las fuerzas paralelas.
Calcula el área de la cara afectada por la fuerza de cizallamiento. Consulta las fórmulas adecuadas para cualquier geometría con la que no estés familiarizado.
Divide la fuerza de corte por la zona de la cara en que ésta actúa. Esta relación es la tensión de cizallamiento. Ésta se distribuye uniformemente sobre una cara, cuando están causadas por las fuerzas que actúan paralelamente a la cara en una sola dirección.
Determina la tensión de cizallamiento. Ésta es la cantidad en que el material se estira en respuesta a la fuerza. Específicamente, bajo una fuerza lineal, la tensión de cizallamiento es igual a la distancia que el material se mueve en la dirección de la fuerza, dividida por la longitud entre la fuerza aplicada y el material de punto de anclaje.
Calcula el módulo de rigidez dividiendo la tensión de cizallamiento en la cara por la tensión de cizallamiento del material. Cuanto mayor sea el módulo de rigidez, más rígido y menos elástico será.
Instrucciones para el torque
Dibuja un diagrama de cuerpo libre eliminando todos los objetos excepto aquel que es de interés.
Suma o resta los torques, dependiendo de la dirección, para encontrar el torque neto que actúa sobre la sección transversal de interés.
Calcula la constante de torsión. La constante de torsión describe cuán resistente es una geometría particular con respecto a la torsión. Consulta las ecuaciones apropiadas para la sección transversal que estés analizando.
Mide la longitud de la distancia de la fuerza de torsión, que actúa en la cara, hasta el punto más cercano de anclaje.
Ten en cuenta el ángulo de giro, el cual es la cantidad que la cara ha girado en relación con el punto más cercano de anclaje.
Calcula el módulo de rigidez. La relación de torsión a la constante de torsión es igual a la relación del producto del módulo de rigidez y el ángulo de giro a la longitud. Puedes resolver esta ecuación para el módulo de rigidez utilizando el álgebra en un par de pasos.