La historia de los exponentes
Escrito por Chuck Ayers ; última actualización: February 01, 2018
La historia generalmente comienza hacia atrás en el principio y luego relaciona el desarrollo de los eventos con el presente para que puedas entender cómo se llegó a donde se está. En matemáticas, en el caso de los exponentes, tiene mucho más sentido empezar con el conocimiento actual y el significado de los exponentes y trabajar hacia atrás hacia el punto desde donde vinieron. En primer lugar, vamos a asegurarnos de que entiendes lo que es un exponente, ya que puede llegar a ser muy complicado. En este caso, vamos a mantenerlo simple.
Dónde estamos ahora
Esta es la versión de la secundaria, de modo que todos deben entender esto. Un exponente refleja un número multiplicado por sí mismo, como 2 veces 2 es igual a 4. En forma exponencial esto se puede escribir 2 ², lo que se denomina como "dos al cuadrado". El elevado es el exponente 2 y el 2 inferior es el número base. Si quieres escribir 2x2x2 puedes escribirlo como 2 ³ o "dos a la tercera potencia". Lo mismo es válido para cualquier número de base, por ejemplo, 8 ² es igual a 8x8 o 64. Ya lo entiendes. Se puede usar cualquier número como base y el número de veces que desees multiplicarlo por sí mismo se convierte en el exponente.
¿De dónde vienen los exponentes?
La palabra en sí misma proviene del latín "expo", que significa "fuera de", y "ponere", que significa "lugar". Si bien la palabra exponente pasó a significar cosas diferentes, el primer uso moderno registrado de exponente en matemáticas fue en un libro llamado "Integra Arithemetica", escrito en 1544 por el autor inglés y matemático Michael Stifel. Pero él simplemente estaba trabajando con una base de dos, de modo que, por ejemplo, el exponente 3 significaba que la cantidad de números 2 que tendrías que multiplicar para obtener 8. Lo que se vería así: 2 ³ = 8. El método de Stifel se diría que es un poco retrógrado en comparación con la forma en que pensamos acerca del tema hoy. Él diría que "el 3 es la configuración del 8". Pero hoy en día, nos referimos a eso simplemente como una ecuación de 2 al cubo. Hay que recordar que él estaba trabajando exclusivamente con una base o un factor de 2 y traduciendo del latín un poco más literalmente de lo que hacemos actualmente.
Aparentes ocurrencias anteriores
Aunque no es 100 por ciento seguro, parece que la idea de elevar al cuadrado o al cubo se remonta hasta el tiempo de los babilónicos. Babilonia era parte de Mesopotamia en la zona que ahora consideramos como Irak. La primera mención conocida de Babilonia se encuentra en una tablilla que data del siglo XXIII a.C. Y lo cierto es que aún así ellos estaban lidiando con el concepto de los exponentes, a pesar de que su sistema de numeración (el sumerio, que ahora es una lengua muerta) utilizaba símbolos para descomponer fórmulas matemáticas. Curiosamente, no sabían qué hacer con el número 0, de modo que lo delineaban como un espacio entre los símbolos.
Cómo se veían los primeros exponentes
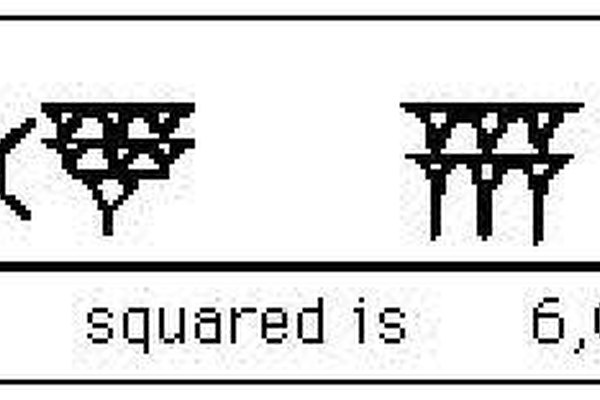
El sistema de numeración era obviamente diferente al de la matemática moderna. Sin entrar en el detalle de cómo y por qué era diferente, basta con decir que escribían el cuadrado de 147 del siguiente modo. En el sistema sexagesimal de las matemáticas, que es lo que los babilonios usaban, el número 147 se escribía 2,27. El cuadrado resultante, que en los tiempos modernos sería el número 21.609, en Babilonia era escrito como 6,0,9. En el sistemas sexagesimal 147 = 2,27 y la cuadratura era el número 21.609 = 6,0,9. Así es como se veía la ecuación, tal como se descubrió en otra tableta antigua. (Trata de poner eso en tu calculadora).
¿Por qué los exponentes?
¿Qué pasa si, por ejemplo, en una fórmula matemática compleja, es necesario calcular algo realmente importante?. Podría ser cualquier cosa y podrías requerir saber a qué es igual 9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9. Imagina colocar todo ese montón de números grandes en un ecuación. ¿No es mucho más fácil escribir 9 ³³? Tú puedes averiguar lo que el número significa si te interesa. En otras palabras, es una forma abreviada, tanto como muchos otros símbolos en matemáticas que son abreviaturas, denotando otros significados y permitiendo escribir fórmulas complejas de una manera más concisa y comprensible. Una advertencia a tener en cuenta. Cualquier número elevado a la potencia cero es igual a 1. Esa es una historia para otro día.




