Actualizado en
18 julio, 2017
¿Qué es el derrame articular en la cadera?
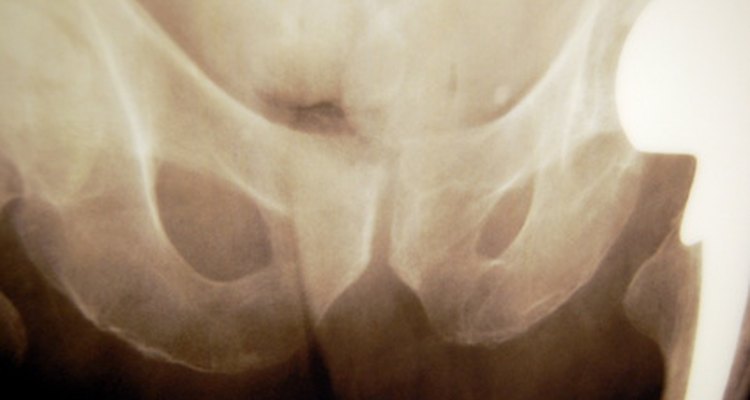
El derrame articular es más comúnmente conocido como agua en la articulación. Pese a que el agua en la rodilla es muy común, también puede haber un derrame articular en la cadera.
Antecedentes
Todas las articulaciones móviles, incluyendo la de la cadera, contiene una cantidad pequeña de líquido sinovial. Esta sustancia ayuda a lubricar las superficies cartilaginosas a fin de que éstas se muevan suavemente, además de nutrir y proteger al cartílago articular.
Demasiado líquido
El derrame articular en la cadera sucede cuando la articulación tiene tanto líquido sinovial que puedes verlo o sentirlo como una hinchazón tensa o dolor. Según el Departamento de Ortopedia y Medicina Deportiva de la Universidad de Washington, una inflamación visible y detectable en la articulación nunca es normal.
Causas
Muchas afecciones pueden producir un derrame articular en la cadera, entre ellas, artritis, traumatismo (el líquido también puede contener sangre), e infección (el líquido puede ser pus).
Diagnóstico
Los rayos X pueden detectar derrames; sin embargo, para determinar si la articulación contiene sangre o pus, es necesario analizar el líquido sinovial.
Tratamiento
De acuerdo con el Departamento de Ortopedia y Medicina Deportiva de la Universidad de Washington, los tratamientos del derrame articular en la cadera dependen de la causa de la acumulación de líquido. Puede ser necesario tomar antibióticos para tratar infecciones o anti-inflamatorios para reducir los efectos de un traumatismo; tal vez sea necesario eliminar líquido de la articulación con un procedimiento denominado aspiración, mediante el cual se inserta una aguja para extraer el fluido. A veces, simplemente se necesita tiempo para que el cuerpo reabsorba el líquido de la articulación.
Más reciente
- hip xray image by JASON WINTER from Fotolia.com