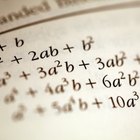Reglas para simplificar polinomios
Escrito por Kylene Arnold ; última actualización: February 01, 2018
Cuando los matemáticos realizan operaciones con polinomios, el resultado suele ser exacto, pero desordenado. Las ecuaciones simplificadas no tienen paréntesis, términos no combinados o exponentes incompletos. Son, como el nombre sugiere, lo más simple que pueden ser. Puedes usar todas las leyes y propiedades que usas en expresiones aritméticas para simplificar polinomios, incluyendo la propiedad distributiva, las leyes de exponentes y la suma y resta de términos.
Paréntesis
Los polinomios simplificados no pueden tener términos entre paréntesis. Debes deshacerte de éstos usando la propiedad distributiva. Esta propiedad dice que a(b + c) = ab + ac. Es decir, puedes simplificar multiplicando el número fuera del paréntesis por cada término del interior. Por ejemplo, en la ecuación 2x^4 + 4(12 + y) - 6y + (4x^2)^2, puedes multiplicar 4 por 12 e "y" para obtener 48 + 4y. La ecuación resultante no necesita el paréntesis que solía contener a esos términos: 2x^4 + 48 + 4y - 6y + (4x^2)^2.
Exponentes
Debes completar todas las operaciones exponenciales para reducir el polinomio. Para hacerlo, debes usar una de las leyes de exponentes. De acuerdo con la ley (x^m)^n = x^mn, para elevar un exponente a una potencia, debes multiplicar los exponentes. Por ejemplo, para simplificar (4x^2)^2, multiplica 2 y 2. El resultado es 4x^4. La ecuación ahora se ve así: 2x^4 + 48 + 4y - 6y + 4x^4.
Combinar términos
Para simplificar un polinomio, debes sumar o restar los términos iguales. Los términos iguales podrían o no tener coeficientes idénticos, pero deben tener variables iguales. Por ejemplo, 2x^4 y 4x^4 o 4y y -6y son series de términos iguales. Nota que si un signo menos precede al término, suele incluirse, como con -6y. Para sumar términos con variables, suma los coeficientes y deja las variables como están. Suma constantes como lo harías en una ecuación aritmética. Por ejemplo, 2x^4 + 4x^4 = 6x^4. Ahora, la ecuación es 6x^4 + 48 - 2y.
Reordenar términos
Aunque el orden de los términos no cambia la respuesta de la ecuación, por costumbre, los matemáticos los escriben en orden alfanumérico, colocando el término de la constante al final. Por ejemplo, 6x^4 + 48 - 2y suele escribirse como 6x^4 - 2y + 48. Si tienes múltiples términos que tienen la misma variable elevada a distintas potencias, ordénalos por sus potencias.