Cómo calcular el coeficiente de regresión
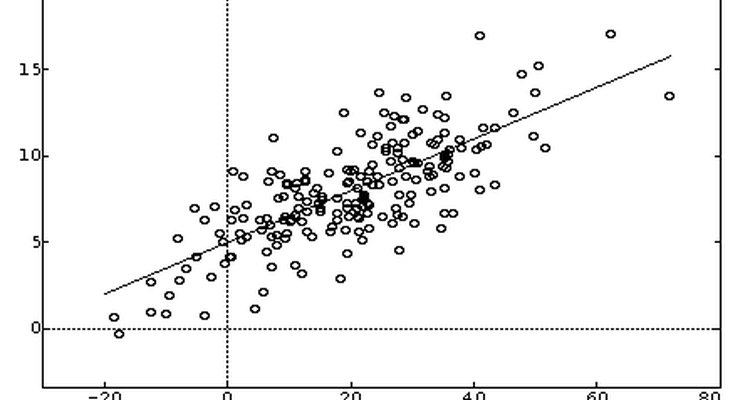
Una de las herramientas básicas para los analistas científicos o ingenieros es el coeficiente lineal. Esta técnica empieza con un juego de datos de dos variables. La variable independiente suele llamarse "x" y la variable dependiente "y". La meta de esta técnica es identificar la línea, y = mx + b, que se aproxima al juego de datos. Esta línea puede mostrar, gráficamente y numéricamente, la relación entre las variables dependiente e independiente. Para este análisis de regresión, un valor para la correlación puede calcularse también.
Step 1
Identifica y separa los valores de x y de y de tus puntos. Si estás usando una hoja de cálculo, ingrésalos en columnas adyacentes. Debería haber el mismo número de valores de x y de y. Si no es así, el cálculo será inexacto o la función de la hoja de cálculo dará error. x = (6, 5, 11, 7, 5, 4, 4) y = (2, 3, 9, 1, 8, 7, 5)
Step 2
Calcula el valor medio de los valores de x y de y dividiendo la suma de todos los valores por el número de valores total en el juego. Estos promedios se llamarán "x_avg" y y_avg". x_avg = (6 + 5 + 11 + 7 + 5 + 4 + 4) / 7 = 6 y_avg = (2 + 3 + 9 + 1 + 8 + 7 + 5) / 7 = 5
Step 3
Crea dos nuevos juegos de datos restando el valor de x_avg de cada valor de x y el valor de y_avg de cada valor de y. x1 = (6 - 6, 5 - 6, 11 - 6, 7 - 6 ... ) x1 = (0, -1, 5, 1, -1, -2, -2) y1 = (2 - 5, 3 - 5, 9 - 5, 1 - 5, ... ) y1 = (-3, -2, 4, -4, 3, 2, 0)
Step 4
Multiplica cada valor de x1 por cada valor de y1, en orden. x1y1 = (0 * -3, -1 * -2, 5 * 4, ... ) x1y1 = (0, 2, 20, -4, -3, -4, 0)
Step 5
Eleva al cuadrado cada valor x1. x1^2 = (0^2, 1^2, -5^2, ... ) x1^2 = (0, 1, 25, 1, 1, 4, 4)
Step 6
Calcula las sumas de los valores x1y1 y x1^2. sum_x1y1 = 0 + 2 + 20 - 4 - 3 - 4 + 0 = 11 sum_x1^2 = 0 + 1+ 25 + 1 + 1 + 4 + 4 = 36
Step 7
Divide "sum_x1y1" por "sum_x1^2" para conseguir el coeficiente de regresión. sum_x1y1 / sum_x1^2 = 11 / 36 = 0.306
Referencias
Consejos
- Para aquéllos que prefieren trabajar directamente con la ecuación, es m = sum[(x_i - x_avg)(y_i - y_avg)] / sum[(x_i - x_avg)^2].
- Muchas hojas de cálculo tendrán una variedad de funciones de regresión lineal. En Microsoft Excel, puedes usar la función de la pendiente en el paso 2, y la hoja de cálculo automáticamente hará los cálculos restantes.






