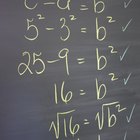Cómo encontrar la magnitud del vector

Photos.com/Photos.com/Getty Images
Un vector es un objeto geométrico que tiene longitud y dirección. Los vectores juegan un papel fundamental en la ciencia porque representan muchas cantidades físicas por ejemplo, la velocidad de un objeto, como un automóvil, es un vector. Cada vector tiene coordenadas o componentes, tales como “X” e “Y". Una magnitud define la longitud del vector. El cálculo de la magnitud se basa en el teorema de Pitágoras y requiere las coordenadas del vector.
Step 1
Eleva la coordenada "X" del vector al cuadrado. Por ejemplo, si el vector tiene las coordenadas (6,-8) entonces 6^2 = 36.
Step 2
Eleva la coordenada "Y" del vector al cuadrado. En este ejemplo, (-8)^2 = 64.
Step 3
Suma los cuadrados de las coordenadas. En este ejemplo, la suma es 36 + 64 =100.
Step 4
Saca la raíz cuadrada de la suma para calcular la magnitud del vector. En este ejemplo, la magnitud es la raíz cuadrada de 100, que es 10.
Sobre el autor
Oxana Fox is a freelance writer specializing in medicine and treatment, computer software and hardware, digital photography and financial services. She graduated from Moscow Medical College in 1988 with formal training in pediatrics.
Créditos fotográficos
Photos.com/Photos.com/Getty Images